Probability Of Poker Hands In Texas Holdem
Probabilities in Texas Hold'em Introduction An understanding of basic probabilities will give your poker game a stronger foundation, for all game types. This article discusses all the important, and interesting, probabilities that you should be aware of. Probabilities in poker Probability means the degree of certainty that a possible event will. 1.7 Figuring out correct Hold’em poker odds without much math; 1.8 Preflop Texas Hold’em Odds; 1.9 Odds of connecting with the Flop in Hold’em; 1.10 Odds On the Flop in Texas Hold’em. 1.10.1 Outs; 1.10.2 Straight and Flush Draw Odds; 1.10.3 On the flop, when you have: 1.11 Odds of hitting a hand by the river from the flop. There are 2,598,960 many possible 5-card Poker hands. Thus the probability of obtaining any one specific hand is 1 in 2,598,960 (roughly 1 in 2.6 million). The probability of obtaining a given type of hands (e.g. Three of a kind) is the number of possible hands for that type over 2,598,960. Thus this is primarily a counting exercise.
Probability Of Poker Hands In Texas Holdemas Hold Em
Both before and after the flop in any limit Holdem game, it is helpful to be able to make a reasonably accurate estimate of the types and numbers of playable hands that you are likely to be competing against.
Much of your decision making involves the business of 'putting' opposing players 'on their hands' (or in other words, figuring out what cards they are playing). Experienced Holdem players are often very good at this. An understanding of the types of hands that are most likely to be against you helps prevent both underestimating and overestimating your competition.

Here are some stats that are based on the total possible combinations of various Holdem hole cards that are normally playable.
For better viewing on your mobile device (or to download or print the chart), check out holdem hole card frequencies in high resolution universal .pdf format.

The five different types of two card Hold'em hands highlighted here are those that are most commonly played. They are not shown in any particular order and within the groups are powerful hands that are almost always played, down to marginal value hands that can be played under certain betting conditions.
The rest of the hands, shown as All Others, are all the very weak hands that most players hardly ever play.
Pairs - All pairs. AA, KK, QQ, JJ, 1010, 99, 88, 77, 66, 55, 44, 33, 22
Two High Cards Suited - AK(S), AQ(S), AJ(S), A10(S), KQ(S), KJ(S), K10(S), QJ(S), Q10(S), J10(S)
Two High Cards Unsuited - AK, AQ, AJ, A10, KQ, KJ, K10, QJ, Q10, J10
Medium and Low Suited Connectors - These include both no-gap and one-gap connectors: J9(S), 109(S), 108(S), 98(S), 97(S), 87(S), 86(S), 76(S), 75(S), 65(S), 64(S), 54(S), 53(S)
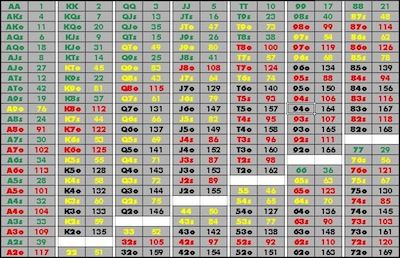
Ace and Non-High Combinations - A9, A8, A7,A6 Note: 25% of these 64 combinations (16) are suited. 75% of the 64 combinations (48) are unsuited.
Introduction
In Texas Hold 'Em a hand is said to be dominated if another player has a similar, and better, hand. To be more specific, a dominated hand is said to rely on three or fewer outs (cards) to beat the hand dominating it, not counting difficult multiple-card draws. There are four types of domination, as follows.

- A pair is dominated by a higher pair. For example J-J is dominated by Q-Q. Only two cards help the J-J, the other two jacks.
- A non-pair is dominated by a pair of either card. For example, Q-5 is dominated by Q-Q or 5-5. In the case of 5-5, three cards only will help the Q-5, the other three queens.
- A non-pair is dominated by a pair greater than the lower card. For example, Q-5 is dominated by 8-8. Only three cards will help the Q-5, the other three queens.
- A non-pair is dominated by another non-pair if there if there is a shared card, and the rank of the opponent's non-shared card is greater the dominated non-shared card. For example Q-5 is dominated by K-5 or Q-7. In the former case (K-5 over Q-5) only three cards can help Q-5, the other three queens.
That said, the following tables present the probability of every two-card hand being dominated, according to the total number of players.
Probability of Domination — PairsExpand
| Cards | 2 Players | 3 Players | 4 Players | 5 Players | 6 Players | 7 Players | 8 Players | 9 Players | 10 Players |
|---|---|---|---|---|---|---|---|---|---|
| 2,2 | 0.0588 | 0.1142 | 0.1659 | 0.2150 | 0.2609 | 0.3044 | 0.3449 | 0.3835 | 0.4195 |
| 3,3 | 0.0540 | 0.1049 | 0.1532 | 0.1983 | 0.2419 | 0.2826 | 0.3212 | 0.3576 | 0.3922 |
| 4,4 | 0.0489 | 0.0956 | 0.1400 | 0.1820 | 0.2220 | 0.2602 | 0.2966 | 0.3313 | 0.3640 |
| 5,5 | 0.0441 | 0.0862 | 0.1265 | 0.1653 | 0.2021 | 0.2376 | 0.2710 | 0.3031 | 0.3345 |
| 6,6 | 0.0392 | 0.0767 | 0.1133 | 0.1481 | 0.1816 | 0.2136 | 0.2448 | 0.2745 | 0.3036 |
| 7,7 | 0.0344 | 0.0675 | 0.0996 | 0.1306 | 0.1605 | 0.1895 | 0.2177 | 0.2447 | 0.2709 |
| 8,8 | 0.0295 | 0.0581 | 0.0858 | 0.1129 | 0.1391 | 0.1648 | 0.1894 | 0.2138 | 0.2369 |
| 9,9 | 0.0246 | 0.0485 | 0.0720 | 0.0947 | 0.1173 | 0.1391 | 0.1604 | 0.1813 | 0.2017 |
| T,T | 0.0196 | 0.0389 | 0.0578 | 0.0765 | 0.0947 | 0.1126 | 0.1300 | 0.1478 | 0.1649 |
| J,J | 0.0147 | 0.0293 | 0.0435 | 0.0577 | 0.0719 | 0.0856 | 0.0992 | 0.1132 | 0.1262 |
| Q,Q | 0.0098 | 0.0195 | 0.0292 | 0.0389 | 0.0483 | 0.0579 | 0.0674 | 0.0766 | 0.0861 |
| K,K | 0.0049 | 0.0098 | 0.0147 | 0.0196 | 0.0245 | 0.0294 | 0.0341 | 0.0391 | 0.0439 |
| A,A | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 |
Probability of Domination — Non-PairsExpand
| Cards | 2 Players | 3 Players | 4 Players | 5 Players | 6 Players | 7 Players | 8 Players | 9 Players | 10 Players |
|---|---|---|---|---|---|---|---|---|---|
| 3,2 | 0.2742 | 0.4785 | 0.6289 | 0.7389 | 0.8187 | 0.8753 | 0.9156 | 0.9438 | 0.9629 |
| 4,2 | 0.2645 | 0.4634 | 0.6124 | 0.7227 | 0.8036 | 0.8626 | 0.9049 | 0.9350 | 0.9562 |
| 4,3 | 0.2496 | 0.4417 | 0.5877 | 0.6986 | 0.7815 | 0.8433 | 0.8888 | 0.9220 | 0.9459 |
| 5,2 | 0.2546 | 0.4487 | 0.5956 | 0.7060 | 0.7881 | 0.8489 | 0.8934 | 0.9255 | 0.9486 |
| 5,3 | 0.2399 | 0.4263 | 0.5701 | 0.6805 | 0.7645 | 0.8279 | 0.8754 | 0.9108 | 0.9367 |
| 5,4 | 0.2253 | 0.4036 | 0.5439 | 0.6539 | 0.7393 | 0.8050 | 0.8556 | 0.8937 | 0.9227 |
| 6,2 | 0.2450 | 0.4338 | 0.5786 | 0.6885 | 0.7718 | 0.8344 | 0.8809 | 0.9152 | 0.9403 |
| 6,3 | 0.2302 | 0.4110 | 0.5525 | 0.6620 | 0.7470 | 0.8118 | 0.8614 | 0.8986 | 0.9266 |
| 6,4 | 0.2154 | 0.3881 | 0.5254 | 0.6344 | 0.7199 | 0.7869 | 0.8394 | 0.8796 | 0.9105 |
| 6,5 | 0.2008 | 0.3647 | 0.4975 | 0.6047 | 0.6911 | 0.7599 | 0.8146 | 0.8581 | 0.8919 |
| 7,2 | 0.2350 | 0.4186 | 0.5611 | 0.6709 | 0.7550 | 0.8191 | 0.8676 | 0.9042 | 0.9311 |
| 7,3 | 0.2204 | 0.3955 | 0.5340 | 0.6430 | 0.7285 | 0.7948 | 0.8461 | 0.8854 | 0.9155 |
| 7,4 | 0.2057 | 0.3724 | 0.5065 | 0.6138 | 0.7000 | 0.7681 | 0.8220 | 0.8642 | 0.8971 |
| 7,5 | 0.1910 | 0.3484 | 0.4776 | 0.5833 | 0.6693 | 0.7388 | 0.7951 | 0.8402 | 0.8761 |
| 7,6 | 0.1763 | 0.3244 | 0.4478 | 0.5510 | 0.6365 | 0.7071 | 0.7651 | 0.8128 | 0.8514 |
| 8,2 | 0.2255 | 0.4034 | 0.5434 | 0.6526 | 0.7375 | 0.8032 | 0.8536 | 0.8923 | 0.9213 |
| 8,3 | 0.2105 | 0.3800 | 0.5157 | 0.6237 | 0.7095 | 0.7771 | 0.8300 | 0.8714 | 0.9034 |
| 8,4 | 0.1959 | 0.3563 | 0.4870 | 0.5932 | 0.6791 | 0.7481 | 0.8037 | 0.8478 | 0.8828 |
| 8,5 | 0.1812 | 0.3323 | 0.4574 | 0.5614 | 0.6467 | 0.7168 | 0.7743 | 0.8208 | 0.8586 |
| 8,6 | 0.1666 | 0.3078 | 0.4272 | 0.5277 | 0.6122 | 0.6829 | 0.7416 | 0.7904 | 0.8311 |
| 8,7 | 0.1518 | 0.2829 | 0.3952 | 0.4922 | 0.5750 | 0.6453 | 0.7056 | 0.7563 | 0.7992 |
| 9,2 | 0.2156 | 0.3878 | 0.5250 | 0.6338 | 0.7194 | 0.7862 | 0.8388 | 0.8793 | 0.9104 |
| 9,3 | 0.2010 | 0.3643 | 0.4968 | 0.6039 | 0.6895 | 0.7583 | 0.8130 | 0.8564 | 0.8904 |
| 9,4 | 0.1862 | 0.3402 | 0.4674 | 0.5720 | 0.6577 | 0.7274 | 0.7843 | 0.8300 | 0.8668 |
| 9,5 | 0.1714 | 0.3157 | 0.4371 | 0.5388 | 0.6234 | 0.6937 | 0.7523 | 0.8003 | 0.8398 |
| 9,6 | 0.1569 | 0.2911 | 0.4061 | 0.5036 | 0.5868 | 0.6573 | 0.7167 | 0.7667 | 0.8088 |
| 9,7 | 0.1419 | 0.2658 | 0.3734 | 0.4669 | 0.5476 | 0.6174 | 0.6776 | 0.7289 | 0.7730 |
| 9,8 | 0.1274 | 0.2403 | 0.3400 | 0.4282 | 0.5061 | 0.5742 | 0.6342 | 0.6867 | 0.7320 |
| T,2 | 0.2057 | 0.3722 | 0.5066 | 0.6143 | 0.7005 | 0.7688 | 0.8229 | 0.8654 | 0.8987 |
| T,3 | 0.1910 | 0.3485 | 0.4772 | 0.5831 | 0.6691 | 0.7387 | 0.7950 | 0.8402 | 0.8762 |
| T,4 | 0.1764 | 0.3240 | 0.4474 | 0.5501 | 0.6352 | 0.7055 | 0.7638 | 0.8111 | 0.8499 |
| T,5 | 0.1617 | 0.2995 | 0.4163 | 0.5153 | 0.5991 | 0.6696 | 0.7286 | 0.7784 | 0.8196 |
| T,6 | 0.1470 | 0.2742 | 0.3843 | 0.4790 | 0.5606 | 0.6305 | 0.6904 | 0.7413 | 0.7847 |
| T,7 | 0.1323 | 0.2487 | 0.3512 | 0.4411 | 0.5196 | 0.5881 | 0.6478 | 0.6996 | 0.7448 |
| T,8 | 0.1176 | 0.2227 | 0.3169 | 0.4008 | 0.4754 | 0.5418 | 0.6009 | 0.6532 | 0.6993 |
| T,9 | 0.1030 | 0.1965 | 0.2817 | 0.3586 | 0.4286 | 0.4923 | 0.5492 | 0.6010 | 0.6473 |
| J,2 | 0.1960 | 0.3566 | 0.4877 | 0.5944 | 0.6808 | 0.7505 | 0.8063 | 0.8508 | 0.8862 |
| J,3 | 0.1813 | 0.3324 | 0.4578 | 0.5617 | 0.6476 | 0.7180 | 0.7757 | 0.8227 | 0.8610 |
| J,4 | 0.1665 | 0.3078 | 0.4271 | 0.5275 | 0.6120 | 0.6828 | 0.7419 | 0.7911 | 0.8317 |
| J,5 | 0.1519 | 0.2827 | 0.3954 | 0.4916 | 0.5741 | 0.6441 | 0.7042 | 0.7549 | 0.7976 |
| J,6 | 0.1371 | 0.2573 | 0.3621 | 0.4537 | 0.5336 | 0.6026 | 0.6625 | 0.7143 | 0.7590 |
| J,7 | 0.1223 | 0.2314 | 0.3284 | 0.4142 | 0.4901 | 0.5572 | 0.6164 | 0.6688 | 0.7145 |
| J,8 | 0.1077 | 0.2050 | 0.2931 | 0.3725 | 0.4442 | 0.5083 | 0.5658 | 0.6174 | 0.6638 |
| J,9 | 0.0931 | 0.1785 | 0.2571 | 0.3289 | 0.3948 | 0.4553 | 0.5100 | 0.5601 | 0.6061 |
| J,T | 0.0783 | 0.1515 | 0.2199 | 0.2837 | 0.3427 | 0.3979 | 0.4493 | 0.4967 | 0.5409 |
| Q,2 | 0.1862 | 0.3406 | 0.4685 | 0.5739 | 0.6604 | 0.7312 | 0.7886 | 0.8352 | 0.8727 |
| Q,3 | 0.1713 | 0.3161 | 0.4379 | 0.5402 | 0.6255 | 0.6968 | 0.7557 | 0.8044 | 0.8445 |
| Q,4 | 0.1568 | 0.2910 | 0.4062 | 0.5045 | 0.5880 | 0.6590 | 0.7189 | 0.7696 | 0.8119 |
| Q,5 | 0.1422 | 0.2658 | 0.3736 | 0.4671 | 0.5482 | 0.6180 | 0.6783 | 0.7299 | 0.7744 |
| Q,6 | 0.1273 | 0.2400 | 0.3400 | 0.4280 | 0.5055 | 0.5734 | 0.6333 | 0.6857 | 0.7312 |
| Q,7 | 0.1126 | 0.2139 | 0.3048 | 0.3868 | 0.4600 | 0.5254 | 0.5835 | 0.6357 | 0.6818 |
| Q,8 | 0.0979 | 0.1875 | 0.2691 | 0.3435 | 0.4113 | 0.4730 | 0.5289 | 0.5800 | 0.6257 |
| Q,9 | 0.0833 | 0.1606 | 0.2321 | 0.2983 | 0.3600 | 0.4166 | 0.4689 | 0.5173 | 0.5619 |
| Q,T | 0.0687 | 0.1332 | 0.1940 | 0.2516 | 0.3052 | 0.3557 | 0.4032 | 0.4480 | 0.4894 |
| Q,J | 0.0540 | 0.1055 | 0.1547 | 0.2020 | 0.2474 | 0.2902 | 0.3313 | 0.3707 | 0.4082 |
| K,2 | 0.1763 | 0.3246 | 0.4491 | 0.5532 | 0.6395 | 0.7111 | 0.7702 | 0.8185 | 0.8579 |
| K,3 | 0.1616 | 0.2998 | 0.4178 | 0.5178 | 0.6027 | 0.6740 | 0.7343 | 0.7848 | 0.8269 |
| K,4 | 0.1469 | 0.2745 | 0.3851 | 0.4808 | 0.5633 | 0.6343 | 0.6948 | 0.7466 | 0.7908 |
| K,5 | 0.1322 | 0.2491 | 0.3517 | 0.4422 | 0.5211 | 0.5904 | 0.6509 | 0.7037 | 0.7494 |
| K,6 | 0.1175 | 0.2230 | 0.3171 | 0.4013 | 0.4763 | 0.5431 | 0.6025 | 0.6550 | 0.7016 |
| K,7 | 0.1029 | 0.1964 | 0.2814 | 0.3586 | 0.4285 | 0.4918 | 0.5490 | 0.6007 | 0.6473 |
| K,8 | 0.0881 | 0.1697 | 0.2447 | 0.3139 | 0.3777 | 0.4367 | 0.4905 | 0.5397 | 0.5853 |
| K,9 | 0.0734 | 0.1423 | 0.2069 | 0.2675 | 0.3238 | 0.3765 | 0.4259 | 0.4720 | 0.5148 |
| K,T | 0.0588 | 0.1146 | 0.1678 | 0.2183 | 0.2665 | 0.3120 | 0.3555 | 0.3961 | 0.4350 |
| K,J | 0.0441 | 0.0866 | 0.1277 | 0.1671 | 0.2058 | 0.2426 | 0.2780 | 0.3125 | 0.3452 |
| K,Q | 0.0294 | 0.0582 | 0.0865 | 0.1141 | 0.1414 | 0.1679 | 0.1940 | 0.2195 | 0.2444 |
| A,2 | 0.1665 | 0.3086 | 0.4294 | 0.5316 | 0.6177 | 0.6901 | 0.7505 | 0.8009 | 0.8425 |
| A,3 | 0.1517 | 0.2835 | 0.3970 | 0.4949 | 0.5791 | 0.6509 | 0.7120 | 0.7641 | 0.8080 |
| A,4 | 0.1372 | 0.2578 | 0.3636 | 0.4565 | 0.5376 | 0.6082 | 0.6695 | 0.7227 | 0.7684 |
| A,5 | 0.1224 | 0.2318 | 0.3294 | 0.4164 | 0.4934 | 0.5618 | 0.6223 | 0.6754 | 0.7225 |
| A,6 | 0.1077 | 0.2054 | 0.2940 | 0.3741 | 0.4462 | 0.5115 | 0.5702 | 0.6228 | 0.6701 |
| A,7 | 0.0931 | 0.1787 | 0.2575 | 0.3300 | 0.3963 | 0.4572 | 0.5129 | 0.5638 | 0.6101 |
| A,8 | 0.0783 | 0.1516 | 0.2200 | 0.2837 | 0.3428 | 0.3983 | 0.4498 | 0.4976 | 0.5418 |
| A,9 | 0.0637 | 0.1241 | 0.1810 | 0.2352 | 0.2866 | 0.3347 | 0.3804 | 0.4237 | 0.4647 |
| A,T | 0.0490 | 0.0959 | 0.1411 | 0.1847 | 0.2264 | 0.2664 | 0.3049 | 0.3417 | 0.3770 |
| A,J | 0.0343 | 0.0677 | 0.1003 | 0.1320 | 0.1629 | 0.1931 | 0.2223 | 0.2507 | 0.2784 |
| A,Q | 0.0195 | 0.0389 | 0.0582 | 0.0769 | 0.0956 | 0.1140 | 0.1320 | 0.1500 | 0.1676 |
| A,K | 0.0049 | 0.0098 | 0.0147 | 0.0195 | 0.0243 | 0.0292 | 0.0340 | 0.0388 | 0.0436 |
Methodology: These tables were created by a random simulation. Each cell in the table above for pairs was based on 7.8 million hands, and 21.7 million for the non-pairs.
2-Player Formula
The probability of domination in a two player game is easy to calculate. For pairs it is 6×(number of higher ranks)/1225. For example, the probability a pair of eights is dominated is 6×6/1225 = 0.0294, because there are six ranks higher than 8 (9,T,J,Q,K,A).
Probability Of Poker Hands In Texas Holdemn Texas Hold Em
For non-pairs the formula is (6+18×(L-1)+12×H)/1225, where
L=Number of ranks higher than lower card
H=Number of ranks higher than higher card
For example, the probability that J-7 is dominated is (6+18×(7-1)+12×3)/1225 = 150/1225 = 0.1224.